MicroDSA: DataStructures and Algorithms

Minimal DSA Reference

Data structures and algorithms represent the core fundamentals of computer science and software design. Below is a minimal reference for a refresher on the topic.

Data Structures

Arrays

• Accessing a value at a given index: O(1)

• Updating a value at a given index: O(1)

• Traverse: O(n) Time, O(1) Space

• Inserting a value at the beginning: O(n)

• Inserting a value in the middle: O(n)

• Inserting a value at the end:

  1) Dynamic Array: O(1)

  2) Static Array: O(n)

• Removing a value at the beginning: O(n)

• Removing a value in the middle: O(n)

• Removing a value at the end: O(1)

• Copying the array: O(n)

Strings

• In most programming languages (C++ is an exception), strings are immutable = can't be edited after creation

• Traverse: O(n) Time, O(1) Space

• Copy: O(n) TS

• Get: O(1) TS

• newString += character is O(n^2) each addition creates an entirely new string

Hash Tables

• Extremely useful for any problem requiring some sort of lookup operation, an array of Linked Lists

• Worse case = Collision of values, assume hash functions optimized and constant-time operations are guaranteed

• Uses a dynamic array of linked lists to efficiently store Key/Value pairs (hash function)

• Inserting a key/value pair: O(1) average, O(n) worse

• Removing a key/value pair: O(1) average, O(n) worse

• Looking up a key: O(1) average, O(n) worse

Stacks and Queues

Stacks

• LIFO (Last In First Out): Stack of books on table, dynamic array, or with a singly linked list

• Pushing an element onto stack: O(1)

• Popping an element off the stack: O(1)

• Peeking at the element on the top of the stack: O(1)

• Searching for an element in the stack: O(n)

Queue

• FIFO (First In, First Out): Line of people, doubly linked list

• Enqueuing an element into queue: O(1)

• Dequeuing an element out of the queue: O(1)

• Peeking at the element at the front of the queue: O(1)

• Searching for an element in the queue: O(n)

Linked Lists

• Node with some value and a pointer to the next node in the linked list (Singly Linked list)

• Accessing the head: O(1)

• Accessing the tail: O(n) (with O(1) for doubly linked list)

• Accessing a middle node: O(n)

• Inserting/Removing the head: O(1)

• Inserting/Removing the tail: O(n) to access + O(1) (with O(1) for doubly linked list)

• Inserting/Removing a middle node: O(n) to access + O(1)

• Searching for a value: O(n)

• Types: Singly List, Doubly List, Circular List, Skip List, Multilevel Lists

Graphs

• Collection of nodes called vertices that might be related to edges

• Types: Graph Cycle, Acyclic Graph, Cyclic Graph, Directed Graph, Undirected Graph, Connected Graph

Trees

• Useful at storing data hierarchically, and for recursion problems

• Terminology: Root, Subtrees, Branches, Leaf Nodes

Binary Trees

• Interior nodes all have two child nodes and leaf nodes all have the same depth

• Can use algorithms like BFS or DFS, values are ordered

• Insert: log(n)

• Remove: log(n)

• Search: log(n)

Min/Max Heaps

• Special case of binary tree, with root smaller/greater or equal to children nodes

• Tree but implemented as array with first element empty, main advantage you can get min/max value in constant time

• Insert: log(n)

• Pop: log(n)

• Min/Max: O(1)

• Heapify(): O(n)

• Building heap iteratively: O(n*logn)

• currentNode = i, childOne -> 2i + 1, childTwo -> 2i + 2, parentNode -> floor((i - 1)//2)

• Node[i], leftChild[2i], rightChild[2i+1]

Tries/Prefix Trees

• Trie is a tree-like data structure that is used to store a dynamic set or associative array where the keys are usually strings

• Benefit of prefix, easy to search for words that start with prefix, useful for autocomplete. Each node can have up to 26 children, one of the characters of the alphabet

• Typically used for efficient retrieval of data associated with keys. Very suitable for tasks such as word lookups, providing auto-complete suggestions, spell-checking, and IP routing

• Insert: O(n)

• Search: O(n)

Math

• 2^0 + 2^1 + 2^2 + 2^3 + .... + 2^n-1 = 2^n - 1 which is O(2^n)

• 1 + 2 + 3 + 4 + .. + n-1 = sum of 1 through n-1 = n(n-1)/2 which is O(n^2)

Complexity

• O(1) < O(logn) < O(n) < O(n*logn) < O(n^2) < O(n^3) < O(2^n) < O(n!)

• Constant: O(1), constant regardless of input size

• Logarithmic: O(log(n)), binary search, as input doubles, operations increment by one unit

• Linear: O(n), scales linearly with input size

• O(ab): traversing through two arrays in two for-loops is not O(n^2) if they are not of the same size.

• Log-Linear: O(n*log(n)), sort an array of size n

• Quadratic: O(n^2)

• Cubic: O(n^3)

• Exponential: O(2^n), recursive runtimes

• Factorial: O(n!)

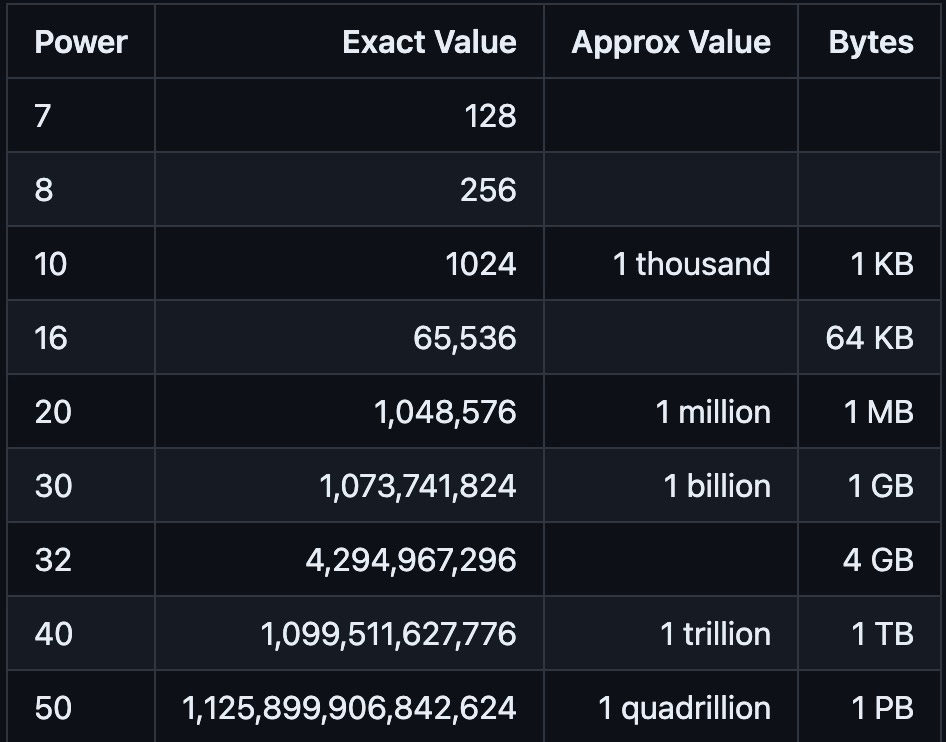
Power of Two Table

Multiples of two, useful for memory estimation

Solution Strategies

1. Invert Binary Tree

2. Reverse Linked List

3. Binary Search

4. Sliding Window (Two Pointers)

5. Recursion (Trees, Graphs, Backtracking, DP)

6. Dynamic Programming

7. Merge & Quick Sort

8. Bit Operations

9. DFS & BFS (usually O(V+E) TS complexity)

10. Heaps

11. Hash Maps

LeetCode Patterns

1. Arrays

   • Common techniques: Hash Tables, Sets, Array Operations

   • Common problems: Duplicates, Numbers Retrieval and Insertion, 2D-Arrays (Traversal, Rotation, Spiral, Product Except Self), Longest Consecutive Sequence

2. Two Pointers

   • Common techniques: Linkedlist, Hash Tables, Array Traversal, Two Indexes, Reduce Time Complexity from O(n^2) to O(n)

   • Common problems: Sorted Lists (Square, Merge), N-sum, Subsequence, Sub-array Product, Sort Objects, Water-Container

3. Sliding Window

   • Common techniques: Traverse with Sub-arrays that Shrink or Expand

   • Common problems: Calculate something over Contiguous Subarrays or Substrings

4. Intervals

   • Common techniques: Involve some kind of Interval, Range, or Period of Time

   • Common problems: Merge/Insert/Non-overlapping Intervals, Meeting Rooms

5. Greedy

   • Common techniques: Local Optimal solution to evolve into Global Optimal

   • Common problems: Optimization, BEST Time to: Buy/Sell Stocks, Schedules, Calendar

6. Dynamic Programming

   • Common techniques: Arrays, Strings, Hash Tables, Trees

   • Common problems: Target Sum, Climbing Stairs, Maximum Product/Subarray, Longest Subsequence/Substring

7. Binary Search

   • Common techniques: Recursive or Iterative

   • Common problems: FIND Smallest Letter/Duplicate/Peak Element/K-Closest Element, SEARCH a 2D/Rotated Matrix

8. Fast & Slow Pointers

   • Common techniques: Traverse Linked-list, Two pointers are initialized at the start of the list. One pointer, the “slow” pointer, moves one step at a time, while the other pointer, the “fast” pointer, moves two steps at a time

   • Common problems: Detecting Cycles in a Linked List, Finding The Middle Element or Kth Element from the End, Remove Linked List Elements

9. Linked Lists

   • Common techniques: Iterative, Recursive, Traversal, Bi-directional, Backward

   • Common problems: Reverse Linked Lists, Rotate Lists, Swap Nodes in Pairs, Reverse Nodes In K-Group

10. Bit Manipulation

    • Common techniques: Shifting Bits Left or Right, Flipping Bits (changing 0 to 1 or 1 to 0), or Combining Numbers with bitwise operations such as AND, OR, XOR, and NOT

    • Common problems: Missing/Counting Numbers, Reverse/Count Bits

11. Graph

    • Common techniques: Traversal, Modification, or Analysis of a Graph

    • Common problems: Clone Graph, Course Schedule, All Paths From Source to Target, Network Delay Time, Minimum Height Tree

12. Depth-First Search

    • Common techniques: Traversing or Searching Trees or Graphs. The algorithm starts at the root and explores as far as possible along each branch before backtracking

    • Common problems: Invert Binary Tree, Path/Target Sum, Min/Max Depth of Binary Tree, Diameter of Binary Tree, Merge Two Binary Trees, Binary Tree Paths, Kth Smallest Element in a BST, Course Schedule, Lowest Common Ancestor of a Binary Tree, Validate Binary Tree Search, Word Search

13. Breadth-First Search

    • Common techniques: Traversing or Searching Trees or Graphs. It starts at the root and explores all the neighbor nodes at the present depth before moving on to nodes at the next depth level

    • Common problems: Invert Binary Tree, Average of Levels In Binary Tree, Min Depth of Binary Tree, Clone Graph, Number of Islands, Minimum Height Trees, Binary Tree Level Order Traversal, Populating Next Right Pointers In Each Node, Course Schedule, Pacific Atlantic Water Flow

14. Sort

    • Common techniques: Bubble, Selection, Insertion, Merge, Quick, Heap, Bucket, Radix, Counting

    • Common problems: Majority Element, Re-order Data in Log Files, Group/Valid Anagrams, Largest Number

15. Stack

    • Common techniques: LIFO, main operations are Push/Pop

    • Common problems: Valid Parentheses, Implementing Stack using Queues, Largest Rectangle in Histogram, Next Greater Element I

16. Queues

    • Common techniques: FIFO, main operations are Enqueue/Dequeue

    • Common problems: Design Circular Queue, Implement Queue using Stacks, Binary Tree Level Order Traversal

17. Heap

    • Common techniques: Min/Max Heap, Insertion/Deletion, usually implemented as Binary Trees

    • Common problems: Kth Smallest Element in Sorted Matrix, Find K Pairs with Smallest Sums, K Closest Points to Origin, Top K Frequent Elements, Kth Largest Element in an Array, Reorganize String, Merge K Sorted Lists, Smallest Range Covering Elements from K Lists, Maximum Frequency Stack, Sliding Window Median, Find Median from Data Stream

18. Trie

    • Common techniques: Known as Prefix Tree, used to store associative data structures, main operations are Insertion/Search/Delete

    • Common problems: Index Pairs of a String, Implement Trie, Longest Word in Dictionary, Word Search II, Maximum XOR of Two Numbers in an Array, Word Search II, Concatenated Words, Prefix and Suffix Search, Palindrome Pairs, Design Search Autocomplete System, Word Squares

Popular Algorithm Problems

1. Traveling Salesman

   • Problem Description: Given a list of cities and the distances between each pair of cities, the problem is to find the shortest possible route that visits each city exactly once and returns to the origin city.

   • Techniques Used: Classic problem in Combinatorial Optimization. Dynamic Programming, Genetic Algorithms, Simulated Annealing, 2-opt and 3-opt heuristics, Graph Theory, and Integer Linear Programming.

2. Floyd-Warshall

   • Problem Description: Given a directed, weighted graph with positive or negative edge weights, the problem is to find the shortest paths between all pairs of vertices in the graph.

   • Techniques Used: Classic problem in Graph Theory and is typically solved using dynamic programming. The Floyd-Warshall algorithm itself is a specific instance of dynamic programming. The key idea is to progressively improve an estimate of the shortest path between any two vertices by considering all possible intermediate vertices.

3. Dijkstra's

   • Problem Description: Given a graph with non-negative weights and a source vertex, the problem is to find the shortest paths from the source to all other vertices in the graph.

   • Techniques Used: Classic example of a Greedy Algorithm. The algorithm uses a priority Queue data structure to continuously select the Vertex with the smallest tentative distance to process next. It also makes use of the property of Relaxation, which ensures that if a path A→B→C is shorter than the known path A→C, it updates the shortest path to A→B→C.

4. Topological Sort

   • Problem Description: Given a directed acyclic graph (DAG), the problem is to find a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering.

   • Techniques Used: Common problem in Graph Theory and is typically solved using Depth-First Search (DFS) or Breadth-First Search (BFS) with a Queue or Stack data structure to keep track of the ordering. The Kahn's algorithm and the DFS-based algorithm are two commonly used methods to solve this problem.

5. Knapsack Problem

   • Problem Description: Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible.

   • Techniques Used: Classic problem in Combinatorial Optimization. Dynamic programming is the most common technique used to solve it. Both the 0/1 version and the fractional version can be solved with variations of dynamic programming.

6. Bellman-Ford Algorithm

   • Problem Description: Given a graph and a source vertex, find the shortest paths from the source vertex to all vertices in the graph. The graph may contain negative weight edges.

   • Techniques Used: The Bellman-Ford algorithm is a single-source shortest-path algorithm. It uses dynamic programming to relax and update the shortest paths.

Links

1. Coding Interviews Resources

2. Design Patterns Resources

3. Systems Design Resources

4. Systems Design Cheatsheet

5. Data Structures and Algorithms Resources

6. Minimal Python Code

7. My Solution to Coding Problems CodeFun

8. MLOps Resources

9. MLOps Tools

10. Machine Learning Interviews Resources

11. Machine Learning Fundamentals

12. Hacker Culture Resources

13. Machine Learning Interview Structure

14. Some cheatsheets for software/robotics/AI